Problem
Code

As far as Advent of Code is concerned, the period from the 19th to the 22nd is what I affectionately like to refer to as the Danger Zone. It's the time when the biggest difficulty spike of the year happens; and often even super invested people that did every task as it came out until then start dropping out.

Well, today's problem delivered.

Part 1

One thing I approve of is that both parts need an idea.

You're given a map (131 by 131 tiles), and you start in the very center of it. The map consists of floor and walls. You're tasked to find the number of tiles you can finish on after taking exactly 64 steps.

The most naive implementation possible is just a floodfill with (x, y, remaining steps) as your "nodes", remembering every unique (x, y, 0) encountered. Though that won't work, because you'd end up processing $4^{64}$ steps. Which is, uh, a lot.

Thankfully, the image provided with in the problem description gives us a big hint:

...........
.....###.#.
.###.##.O#.
.O#O#O.O#..
O.O.#.#.O..
.##O.O####.
.##.O#O..#.
.O.O.O.##..
.##.#.####.
.##O.##.##.
...........

You can stop on every other tile. And when you think about it, it makes sense—whenever your remaining step count is even, that means you're on a tile you could end up on, because you can simply waste all your remaining steps by walking back and forth.

With this little extra details, we can massively improve the efficiency of our floodfill—always take 2 steps at a time, and every tile we land on automatically counts.

fn floodfill(map: &[&[u8]], start: &[(usize, usize)], steps: usize) -> usize {
    let mut queue = VecDeque::from_iter(start.iter().map(|&s| (s, steps / 2)));
    let mut found = HashSet::new();
    while let Some(((x, y), remaining)) = queue.pop_front() {
        if !found.insert((x, y)) || remaining == 0 {
            continue;
        }
        let open = |dx: i32, dy: i32| {
            let Ok(x) = usize::try_from(x as i32 + dx) else {
                return false;
            };
            let Ok(y) = usize::try_from(y as i32 + dy) else {
                return false;
            };

            !found.contains(&(x, y))
                && matches!(map.get(y).and_then(|line| line.get(x)), Some(b'.' | b'S'))
        };

        let (left, up, right, down) = (open(-1, 0), open(0, -1), open(1, 0), open(0, 1));
        let dirs = [
            (left, -2, 0),
            (left || up, -1, -1),
            (up, 0, -2),
            (up || right, 1, -1),
            (right, 2, 0),
            (right || down, 1, 1),
            (down, 0, 2),
            (down || left, -1, 1),
        ];

        for (reachable, dx, dy) in dirs {
            if reachable && open(dx, dy) {
                queue.push_back((
                    ((x as i32 + dx) as usize, (y as i32 + dy) as usize),
                    remaining - 1,
                ));
            }
        }
    }

    found.len()
}

It's a little bit fiddly, but a simple floodfill(&map, &[start], 64) gives us the result. It's not the most efficient thing I've ever written, but it does the job.

Part 2

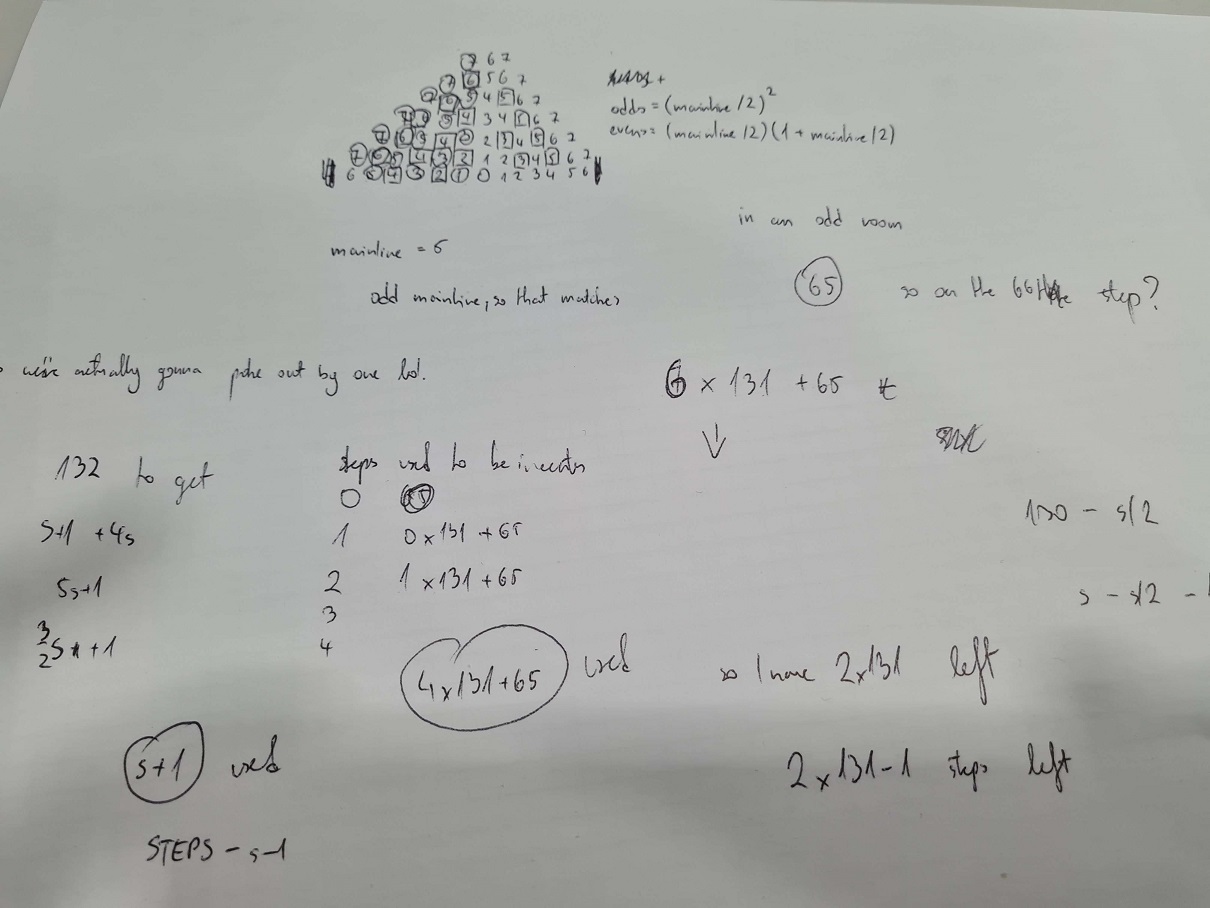
One of the many pages of paper I filled doing this. The code I ended up with isn't too big, though:

pub fn two(input: &str) -> crate::Result<usize> {
{
    const STEPS: usize = 26501365;
    let map: Vec<_> = input.linesas_bytes).collect(;
    let s = map.len();

    let mainline = (STEPS - map.len() / 2) / map.len() - 1;
    let (mainline_evens, mainline_odds) = ((mainline + 1) / 2, mainline / 2);

    let quarter_odds = (mainline / 2) * (mainline / 2);
    let quarter_evens = (mainline / 2) * (1 + mainline / 2);
    let quarter_edge_close = mainline;
    let quarter_edge_far = quarter_edge_close + 1;

    let total_evens = 4 * (mainline_evens + quarter_evens);
    let total_odds = 1 + 4 * (mainline_odds + quarter_odds);

    let center: &[(usize, usize)] = &[(s / 2, s / 2)];
    let middles = &[
        (0, s / 2),
        (s / 2, 0),
        (s - 1, s / 2),
        (s / 2, s - 1),
    ];
    let corners = &[
        (0, 0),
        (s - 1, 0),
        (s - 1, s - 1),
        (0, s - 1),
    ];
    
    let combinations = [
        (total_odds, center, true, None),
        (total_evens, center, false, None),
        (1, middles, false, Some(s - 1)),
        (quarter_edge_close, corners, true, Some(3 * s / 2 - 1)),
        (quarter_edge_far, corners, false, Some(s / 2 - 1)),
    ];

    let mut total = 0;
    for (count, starts, odd_steps, step_limit) in combinations {
        for &(x, y) in starts {
            let mut starts = vec![];
            if odd_steps {
                if x > 0 {
                    starts.push((x - 1, y));
                }
                if x < (s - 1) {
                    starts.push((x + 1, y));
                }
                if y > 0 {
                    starts.push((x, y - 1));
                }
                if y < (s - 1) {
                    starts.push((x, y + 1));
                }
            } else {
                starts.push((x, y));
            }

            let steps = step_limit.map(|s| s - s % 2).unwrap_orMAX;
            let tiles = floodfill(&map, &starts, steps);

            total += count * tiles;
        }
    }
    Ok(total)
}
}

The task is now upgraded: The map wraps infinitely, and you get 26501365 steps. That's 26 and a half million. Even with an insanely optimized flood fill, you're not doing this. Instead I came up with an intricate scheme to reduce work. How do I know it's intricate? My actual code is significantly more comments than code.

The multiple pages of scribbles I produced were all in the service of deriving formulas and relationships between numbers, so that I could produce the right number of rooms, and I ended up with surprisingly little code:

The map is peculiar

Looking at the actual map (which I won't reproduce here, but you can easily check yourself!), there's three very suspicious things of note:

• from the center, you can go in a straight line in any direction to reach the edge of the map without obstruction (I call this "the main cross");
• there's a huge hollowed-out diamond (I don't think it super matters, but it does look suspicious);
• the edge of the map is entirely hollowed out.

From these, we can infer a very important idea: On any given map, we can go from the center to any point on the edge (and vice versa) in an optimal amount of steps, without ever running into any obstacles. This lets us ignore a lot of details about the map.

The step count is peculiar

It may not be immediately obvious, but it's fairly easy to notice once you start implementing anything: 26501365 modulo 131 (the actual size of the map) is 65 (half the size of the map). So, if you went in a straight line, say, to the right, for all 26501365 steps, you'd end up exactly at the far edge of a map.

This is important. We already know from part 1 and various visualisations that the final solution will be roughly diamond-shaped—and with this extra final fact, we know the exact shape.

Repetition

Now, the idea I came up with is fairly simple: Find all maps we ever touch at all (relatively easy to do with some number manipulations); categorize those maps based on how they're filled, and then for each category run the actual floodfill once, multiply it by the number of copies of that map, and then sum all of that. Easy!

Totally.

There's two main areas of interest: half-axes, and quarters. Because the whole thing is a diamond, we have four of each, and each mirroring is handled roughly the same way.

Parity

There's one more concept I want introduce for now. Let's say we have completely empty 3x3 maps, and mark valid squares on them:

+---+---+
|O O| O |
| O |OSO|
|O O| O |
+---+---+

I call a map "even" if the center tile is a valid ending tile, "odd" if it isn't. So in the example I posted, the left one is even, the right one is odd. This is important, because adjacent maps will always be of opposite parity. I can't really fully prove that, but I hope it makes intuitive sense when you look at the image above.

Note that the step count in part 2 is odd, so the starting map is odd, because the starting tile isn't a valid ending tile.

Half-axes

A "half-axis" is what I call when you just go in a straight line until you run out of steps. We have four of them: negative x (left), negative y (up), positive x (right), and positive y (down). Assuming a completely empty 7x7 map, going to the right might look something like this:

+-------+-------+-------+-------+-------+
| O O O |O O O O| O O O |O O O O| O O   |
|O O O O| O O O |O O O O| O O O |O O O  |
| O O O |O O O O| O O O |O O O O| O O O |
|O OSO O| O O O |O O O O| O O O |O O O O|
| O O O |O O O O| O O O |O O O O| O O O |
|O O O O| O O O |O O O O| O O O |O O O  |
| O O O |O O O O| O O O |O O O O| O O   |
+-------+-------+-------+-------+-------+

I did, uuuh, 31 steps here, I think. Note how the second and fourth map are identical. If we went 14 more steps, it would add another copy of the second and third map, each. I call these "mainline evens" and "mainline odds".

let mainline = (STEPS - map.len() / 2) / map.len() - 1;
let (mainline_evens, mainline_odds) = ((mainline + 1) / 2, mainline / 2);

For STEPS = 31, this would result in:

• mainline = 3
• mainline_evens = 2
• mainline_odds = 1

This matches what we've counted up there exactly. With 14 more steps, we'd have 5, 3, and 2, respectively.

Then, at the very end, we have one more map that's partially-filled.

And that's it, we've successfully categorized and counted the number of maps along one half-axis. Later on we'll have to use these numbers four times, once for each half-axis.

Quarters

It's probably not very controversial to say that there's 4 quarters. We'll only be looking at one though, the bottom right one. Here's an overview of the bottom right, zoomed out to look at the "super map" of maps. Each character is one map:

+------
|OEOEoe
|EOEoe
|OEoe
|Eoe
|oe
|e

Each uppercase O is a completely-filled odd map; each uppercase E is a completely-filled even map. The lowercase ones are partially-filled. Crucially, however, they're all partially-filled in the exact same way. That is, each lowercase o is identical, and each lowercase e is identical.

You can count the number of each of them with simple calculations.

Notice that completely-filled odd rooms (uppercase O) show up in a pattern; there's 1 one maps away from center, and 3 of them three steps away from center. This pattern would continue; it's the sum of all odd numbers less than mainline, except for the last one. The sum of the first $n$ odd numbers is $n^2$, which is pretty cool.

Similar with completely-filled even rooms (uppercase E)—it's the sum of all even numbers less than mainline. The sum of the first $n$ even numbers is $n(n+1)$. That's because it's the same as twice the sum of just the first $n$ natural numbers, and we have a formula for that.

There's mainline lowercase os, and one more es than that. Easy.

let quarter_odds = (mainline / 2) * (mainline / 2);
let quarter_evens = (mainline / 2) * (1 + mainline / 2);
let quarter_edge_close = mainline;
let quarter_edge_far = quarter_edge_close + 1;

And now, we've actually finished counting every map!

Putting it all together

We now officially have 14 categories of rooms. I'm gonna list each one:

• completely-filled even;
• completely-filled odd;
• western partially-filled mainline;
• northern partially-filled mainline;
• eastern partially-filled mainline;
• southern partially-filled mainline;
• northwestern partially-filled close/odd;
• northwestern partially-filled far/even;
• northeastern partially-filled close/odd;
• northeastern partially-filled far/even;
• southeastern partially-filled close/odd;
• southeastern partially-filled far/even;
• southwestern partially-filled close/odd;
• southwestern partially-filled far/even;

For each of those categories, we have a count and the knowledge that they're identical. So we now simply need to run a flood fill once for each.

let center: &[(usize, usize)] = &[(s / 2, s / 2)];
let middles = &[
	(0, s / 2),
	(s / 2, 0),
	(s - 1, s / 2),
	(s / 2, s - 1),
];
let corners = &[
	(0, 0),
	(s - 1, 0),
	(s - 1, s - 1),
	(0, s - 1),
];

let combinations = [
	(total_odds, center, true, None),
	(total_evens, center, false, None),
	(1, middles, false, Some(s - 1)),
	(quarter_edge_close, corners, true, Some(3 * s / 2 - 1)),
	(quarter_edge_far, corners, false, Some(s / 2 - 1)),
];

This part declares all 14 categories, how they're entered, and how many steps are left available when entering them. I no longer have the power left to go into detail on how I derive all of those bools and numbers, but between this post and the comments in the original code, it should be possible to get there for those that really wanna know.

Overall, cool task. I cannot tell you the satisfaction of running your code for the first time on real data, getting a 15 digit result, pasting it over, and it's correct.